What is Linear Data Structure? | Introduction to Linear Data Structure

In linear data structures, the elements are arranged in a sequence one after the other. These are single level data structures, having their elements in a sequence. Since elements are arranged in particular order, they are easy to implement. In linear data structure, data is stored in memory in a linear fashion.

Examples of linear data structure are: Array, Stack, Queue and Linked List.

ARRAY:

An array is a fixed size linear data structure. It is a collection of items of same data type stored at contiguous memory locations.

Array is a collection of homogeneous (similar type) data elements. It's elements are stored in computer memory in a linear fashion. The elements of an array can be identified by using its index value. The smallest index value of an array is called its lower bound and the highest index value is called its upper bound.

The index value of the starting element of an array will be 0. So if we declare an array of size 6, then the index value of the elements in an array will be from 0 to 5. Lower bound is 0 and upper bound is 5.

• Array Index: The location of an element in an array has an index, which identifies the element. Array index starts from 0.
• Array element: Items stored in an array is called an element. The elements can be accessed via its index.

Arrays can of following types:

(i)   One Dimensional Array

(ii)  Two Dimensional Array

One-Dimensional Arrays:

One-dimensional array is also called as single dimension array. In one dimensional array, each element is represented by one subscript. The elements are stored in consecutive memory locations. E.g. A [1], A [2], …, A [N].

A one dimensional array is used when it is used when it is necessary to keep a large number of items in memory and reference all the items in a uniform manner.

 

Two-Dimensional Arrays:

The Two Dimensional array is used for representing the elements of the array in the form of the rows and columns. A two dimensional array is a logical data structure that is useful in programming and problem solving. For example, such an array is useful in describing an object that is physically two dimensional, such as a map or a checkerboard. It is also useful in organizing a set of values that are dependent upon two inputs. For example, a program for a department store that has 20 branches, each of which sells 30 items, might include a two dimensional array declared by

int sales[20][30];

In two dimensional arrays, each element is represented by two subscripts. Thus a two dimensional m x n array A has m rows and n columns and contains mxn elements. It is also called matrix array because in it the elements form a matrix. E.g. A [2] [3] has 2 rows and 3 columns and 2*3 = 6 elements. Two-dimensional array will be accessed by using the subscript of row and column index.

Applications of Arrays:

 

1. Arrays are used to store data elements of same type in a specific order. For example, an array can be used to store the marks of a student.

2. Arrays help to maintain large data under a single variable name. This avoids the confusion of using multiple variables.

3. Arrays can be used for sorting data elements. Different sorting algorithms like the Bubble sort, Insertion sort, Selection sort, Merge sort, Quick sort etc. use arrays to store and sort elements.

4. Various mathematical problems like matrices can be easily and efficiently solved with the help of an array data structure.

5. Database records are usually implemented by the array. Many databases small and large consist of one-dimensional and two dimensional arrays whose elements are records.

6. Arrays can be used for CPU scheduling. In CPU scheduling, we need to maintain a list of all the processes that need to be scheduled, arrays can be a useful data structure to store this list of processes.

7. Arrays are used to implement other data structures like stacks, Queues, Heaps, Hash tables etc.

8. Arrays can be used to represent graphs in computer science. Each element in the array represents a node in the graph, and the relationships between the nodes are represented by the values stored in the array.

9. Two dimensional arrays, commonly known as, matrices, are used in image processing.

10. Arrays can be used in speech processing, where every speech signal is an array.

STACK:

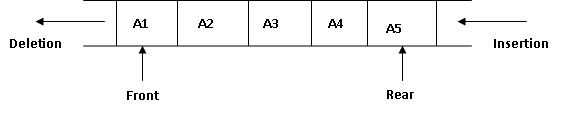
Stack is defined as a list in which all the insertions and deletions operations are performed at one end called the TOP. It is like a container.  A stack operates according to the Last In First out (LIFO) principle, which states that the element that was added last will be deleted first.

 

It is an ordered collection of items into which new items may be inserted and from which items may be deleted at one end. Stack is used to store an ordered, linear sequence of elements.

Fig: Representation of a Stack

In stack, the information is processed in LIFO (Last In First Out) way. It means that the last element inserted into a stack is the first element to be deleted.

For example, stack of dishes, stack of folded towels, Pile of books, the stack of trays in a cafeteria etc.

 

Stack Operation:

 

      · PUSH

      · POP

      · PEEK

PUSH: The insertion operation is known as PUSH. When an item is added to a stack, it is pushed onto the stack. The top of the stack is always where a new element is added, so we must always check to see if it is empty by using the formula TOP=Max-1. In the case that this condition is false, the Stack is full and no other elements may be added. Even if we attempt to add the element, a Stack overflow message will be shown.

 

Algorithm:

Step-1: If TOP = Max-1
Print “Overflow”
Goto Step 4
Step-2: Set TOP= TOP + 1
Step-3: Set Stack[TOP]= ELEMENT
Step-4: END

 

POP: The deletion operation is known as POP. When an item is deleted from a stack, it is popped from the stack. POP denotes removing a stack element. Make sure to verify that the Stack Top is NULL, i.e., TOP=NULL, before deleting an element. In the event that this condition is met, the Stack will be empty, making deletion operations impossible. Even if deletion attempts are made, the Stack Underflow warning will be produced.

Algorithm:

Step-1: If TOP= NULL
Print “Underflow”
Goto Step 4
Step-2: Set VAL= Stack[TOP]
Step-3: Set TOP= TOP-1
Step-4: END

 

 

PEEK:  The Peek operation is employed when it is necessary to return the value of the topmost stack element without erasing it. This operation first determines whether the Stack is empty, i.e., TOP = NULL; if it is, then the value will be returned; otherwise, an appropriate notice will be displayed.

Algorithm:

Step-1: If TOP = NULL
PRINT “Stack is Empty”
Goto Step 3
Step-2: Return Stack[TOP]
Step-3: END

Application of Stack:

 

1. Stacks can be used for Evaluation of Arithmetic Expressions. In computer languages, a stack is an extremely efficient data structure for evaluating arithmetic expressions.

2. Stacks can be used for Processing Function (Subprogram) Calls.

3. Stacks can be used to check parenthesis matching in an expression.

4. Stacks can be used for Evaluation of postfix Expressions.

5. It can also be used to convert one form of expression to another form. For example, converting Infix to Postfix or Infix to Prefix.

6. Recursion is one of the important applications of stack.

7. Stacks can be used for systematic Memory Management.

8. Stack is used in depth first search in graph and tree traversal.

9. The simplest application of a stack is to reverse a string. We push the characters of string one by one into stack and then pop character from stack.

10. Another application of stack is UNDO and REDO functions in text editors; these operations are accomplished by keeping all text changes in a stack.

11. Stack is also heavily used for Syntax Parsing by most of the Compilers.

12. Stack data structures are used in Backtracking problems. In backtracking, while finding the every possible solution of a problem, we store the solution of a previously calculated problem in stack and use that solution to solve the upcoming problems.

Evaluation of Arithmetic Expressions:

In computer languages, a stack is an extremely efficient data structure for evaluating arithmetic statements. Operands and operators are the components of an arithmetic expression.
The arithmetic expression may additionally contain parenthesis such as "left parenthesis" and "right parenthesis," in addition to operands and operators.

Example: A + (B – C)
The normal precedence rules for arithmetic expressions must be understood in order to evaluate the expressions. The following are the five fundamental arithmetic operators’ precedence rules:

Operators	Associativity	Precedence
^ , Exponentiation	Right to left	Highest followed by *Multiplication and /division
*Multiplication, /division	Left to right	Highest followed by + addition and – subtraction
+ addition, – subtraction	Left to right	lowest

Notations for Arithmetic Expression:

There are three notations to represent an arithmetic expression:

      · Infix Notation

      ·  Prefix Notation

      ·  Postfix Notation

 

Infix Notation:

Each operator is positioned between the operands in an expression written using the infix notation. Depending on the requirements of the task, infix expressions may be parenthesized or not.

Example: A + B, (C – D) etc.

Because the operator appears between the operands, all of these expressions are written in infix notation.

 

Prefix Notation:

The operator is listed before the operands in the prefix notation. Since the Polish mathematician invented this system, it is frequently referred to as polish notation.

Example: + A B, -CD etc.

Because the operator occurs before the operands in all of these expressions, prefix notation is used.

 

Postfix Notation:

The operator is listed after the operands in postfix notation. Polish notation is simply reversed in this notation, which is also referred to as Reverse Polish notation.

Example: AB +, CD+, etc.

All these expressions are in postfix notation because the operator comes after the operands.

QUEUE:

Queue is a linear data structure that follows the First-In-First-Out (FIFO) principle. It is a list or collection of items in which insertions occurs from one end known as the rear end or the tail of the queue, whereas deletion occurs from the other end known as the front end or the head of the queue.

 

Unlike stacks, a queue is open at both ends. One end is always used to insert data (enqueue) and the other end to remove data (dequeue).

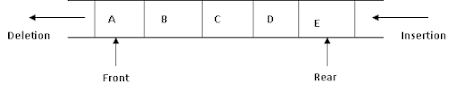
Fig: Representation of a Queue

Above figure illustrates a queue containing five elements A, B, C, D, and E. A is at the front of the queue and E is at the rear.

In queue, the information is processed in FIFO (First In First Out) or FSFS (First Come First Served) way. It means that the first element to be inserted in the queue will be the first element to be deleted or removed from the queue. The process of inserting items in queue is called “enqueueing” and removing items from a queue is called “dequeueing”.

Examples of a queue around in the real world- A line at a bank or at a bus stop, a line of people waiting to purchase tickets are all familiar example of queues.

There are four types of queues in data structure:

• Simple Queue or Linear Queue
• Circular Queue
• Double Ended Queue (Dequeue)
• Priority Queue

Simple or Linear Queue:

A Simple or Linear Queue is a basic queue. In this queue, insertion takes place from one end while deletion takes place from the other end. The end at which the insertion takes place is known as the rear end, and the end at which the deletion takes place is known as front end. It strictly follows the FIFO (First in First out) rule.

The major drawback of a linear queue is that insertion is done only from the rear end (back end). If the first three elements are deleted from the queue, we cannot insert more elements even though the space is available in a Linear Queue. In this case, the linear Queue shows the overflow condition as the rear is pointing to the last element of the Queue.

Circular Queue:

A circular queue is a type of a queue in which the last element is followed by the first element. It is similar to the linear queue except that the last element of the queue is connected to the first element. In circular queue, the last element points to the first element making a circular link. As a result, a circle-like structure is formed.

A circular queue is the extended version of a regular queue where the last element is connected to the first element. Circular Queue is also known as Ring Buffer.

A circular queue can do what a linear queue can’t. The drawback that occurs in a linear queue is overcome by using the circular queue. If the empty space is available in a circular queue, the new element can be added in an empty space by simply incrementing the value of rear.


The main advantage of a circular queue over a simple queue is better memory utilization. If the last position is full and the first position is empty, we can insert an element in the first position. This is not possible in a linear queue.

Priority Queue:

A priority queue is a special type of queue in which each element has a priority associated with it. This priority determines which elements are to be deleted and processed first. There can be different criteria’s for the priority queue to assign priorities.

Priority queue assigns a priority to each element. Inserting and removing of elements from queue is decided by the priority of the elements. An element of the higher priority is processed first. If elements with the same priority occur, they are served according to their order in the queue. 

There are two types of priority queue:

Ascending Priority Queue:

In this priority queue, the elements are arranged in ascending order of their priority, i.e., the element with the smallest priority comes at the start, and the element with the greatest priority comes at the end.

 

Descending Priority Queue:

In this priority queue, the elements are arranged in descending order of their priority, i.e., the element with the greatest priority is at the start and the element with the smallest priority is present at the end of the queue.

Double Ended Queue (Deque):

A double-ended queue or deque, is a type of queue that allows elements to be added or removed from either end of the queue. In a standard queue, insertion can only be done from the back (rear) and deletion only from the front. A double-ended queue allows for insertion and deletion from both ends.

Types of Deque:

• Input Restricted Dequeue
• Output Restricted Dequeue

 

 

Input Restricted Deque:

As the name implies, in input restricted queue, insertion operation can be performed at only one end, while deletion can be performed from both ends.

Output Restricted Deque:

 

As the name implies, in output restricted queue, deletion operation can be performed at only one end, while insertion can be performed from both ends.

Application of Queue:

 

1. Queue is used for managing requests on a single shared resource such as CPU scheduling and disk scheduling.

2. Queues can be used to manage and allocate resources, such as printers or CPU processing time.

3. All types of customer service (like railway reservation) centers are designed using the concept of queues. Call center phone systems use queues to hold people calling them in order until a service representative is free.

4. Queues are used in asynchronous transfer of data. When data is transferred asynchronously between two processes, queue is used for synchronization. For example: IO Buffers, file IO, etc.

5. Web servers use queues to manage incoming requests from clients. Requests are added to the queue as they are received, and they are processed by the server in the order they were received.

6. Nowadays computer handles multiuser, multiprogramming environment and time-sharing environment. In such an environment a system (computer) handles several jobs at a time. To handle these jobs the concept of a queue is used.

7. Queues are used for operation on data structure. Certain operations like tree traversal and breadth first search uses queue for traversal.

8. Queues are used as a buffer space in network, during transmission of data from source to destination.

9. Queues are used as buffers in most of the applications like MP3 media player, CD player, etc.

10. Routers and mail queues are examples of queue applications in computer networks.

 

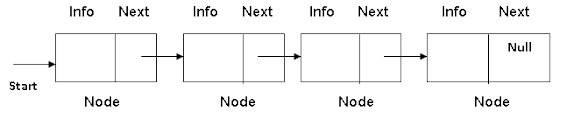
Linked List:

 

It is defined as a linear collection of data elements called nodes, where each node consists of two parts i.e., information and pointer to next node (next node address). The information part holds the actual element on the list. A list pointer variable FIRST or START contains the address of the first node in the list. The last node contains NULL pointer. This null pointer is used to signal the end of a list.

Fig: Representation of a Linked List

Linked list is a dynamic data structure. The number of nodes on it may vary as elements are inserted and removed. It is possible to grow and shrink the size of linked list at any time. A linked list is a chain of structures in which each structure consists of data as well as pointers, which store the address (link) of the next logical structure in the list. The linked list with no nodes on it is called the NULL list or the Empty list.

Types of Linked List:

There are different types of linked list. These are given below:

 

(i)    Singly Linked List

(ii)   Doubly or two-way Linked List

(iii)  Circular Linked List

(iv)  Circular Doubly Linked List

Singly Linked List: In a singly linked list each node contains data or information and a single link, which attaches it to the next node in the list.

Circular Linked List: Linked list structure in which the last element point to the first element of the lists is called circular linked list. A circular linked list contains a pointer from the last node to the first node. In fact, there is no first or last nodes, as all the nodes are linked in a circular way.

Doubly Linked List: In a doubly linked list each node contains data and two links, one to the previous node and one to the next node.

Circular Doubly Linked List: Circular Doubly Linked List has properties of both doubly linked list and circular linked list in which two consecutive elements are linked or connected by previous and next pointer and the last node points to first node by next pointer and also the first node points to last node by the previous pointer.

Application of Linked List:

1. Linked list is used in memory management.

2. Linked list is used in programming requiring dynamic memory allocation.

3. We can use linked lists for performing arithmetic operations on long int.

4. We can implement data structures like stacks and queues with the help of a linked list.

5. Linked list is used in the implementation of graphs. Linked List helps in storing the adjacent vertices of a graph in adjacency list representation.

6. In the browser, when we want to use the back or next function to change the tab, it used the concept of a doubly-linked list.

7. Symbol table management in compiler design uses linked list.

8. Advance scientific calculation and numerical analysis using sparse matrices. The sparse matrix is represented by linked list.

9. Polynomials can be represented with the help of linked list.  Each term in a polynomial has coefficient and power (exponent). Coefficient and power are stored as nodes and pointer point to the next node.

10. Linked List is used to implement hash tables. It is used to prevent collision in hashing.