Data Structure:
The data structure describes the way the data is organized and stored in memory for the convenience of processing.A data structure refers to an organized way of arrangement of data, related to each other in the memory which allows the program to handle the data in an efficient way.
A data structure can be represented as follows:
Data Structure= organized data + allowed operationA Data Structure is a logical way of organization data that considers not only the items stored, but also their relationship to each other.
For example consider a single dimensional array in C language declared as follows:
int a[5];
In this structure ‘a’ contains 5 integer values. The index subscripting starts from 0 i.e., a[0] and ends with 4, a[4]. The array elements are accessed by their index positions.
A data structure is a logical method of representing data in memory using the simple and complex data types provided by the language.
Types of Data Structure:
Basically, there are two types of data structures:
- Linear data structure
- Non-linear data structure
Fig: Different types of data structures
Linear Data Structures:
In linear data
structures, the elements are arranged in a sequence one after the other. These are single level data
structures, having their elements in a sequence.
Since elements are arranged in particular order, they are easy to
implement. In linear data structure, data is stored in
memory in a linear fashion.
Examples of linear data structure are: Array, Stack, queue and Linked List.
Array:
An array is a fixed size
linear data structure. It is a collection of
items of same data type stored at contiguous memory locations.
Array is a collection of
homogeneous (similar type) data elements. It’s elements are stored in computer
memory in a linear fashion. The elements of an array can be identified by using its index
value. The index value of the starting element of an array will be 0. So if we
declare an array of size 6, then the index value of the elements in an array
will be from 0 to 5.
- Array Index: The location of an element in an array has an
index, which identifies the element. Array index starts from 0.
- Array element: Items stored in an array is called an
element. The elements can be accessed via its index.
Arrays can of following types:
(i) One
Dimensional Array
(ii) Two
Dimensional Array
One Dimensional Array: One-dimensional array is also called as single dimension array. A one-dimensional array is used when it is necessary to keep a large number of items in memory and reference all the items in a uniform manner.
In one dimensional array, each element is represented by one subscript.
The elements are stored in consecutive memory locations. E.g. A [1], A [2],
….., A [N].
In two dimensional array, each element is represented by two subscripts. Thus a two dimensional m x n array A has m rows and n columns and contains mxn elements. It is also called matrix array because in it the elements form a matrix. E.g. A [2] [3] has 2 rows and 3 columns and 2*3 = 6 elements. Two-dimensional array will be accessed by using the subscript of row and column index.
Applications of Arrays:
1. Arrays are used to store data
elements of same type in a specific order. For example, an array can be used to
store the marks of a student.
2. Arrays help to maintain large data
under a single variable name. This avoids the confusion of using multiple
variables.
3. Arrays can be used for sorting data
elements. Different sorting algorithms like the Bubble sort, Insertion sort,
Selection sort, Merge sort, Quick sort etc. use arrays to store and sort
elements.
4. Various
mathematical problems like matrices can be easily and
efficiently solved with the help of an array data structure.
5. Database records are usually
implemented by the array. Many databases small and large consist of
one-dimensional and two dimensional arrays whose elements are records.
6. Arrays can
be used for CPU scheduling. In
CPU scheduling, we need to maintain a list of all the processes that need to be
scheduled, arrays can be a useful data structure to store this list of
processes.
7. Arrays are used to implement other
data structures like stacks, Queues, Heaps, Hash tables etc.
8. Arrays can be used to represent
graphs in computer science. Each element in the array represents a node in the graph, and
the relationships between the nodes are represented by the values stored in the
array.
9. Two dimensional arrays, commonly known as, matrices, are used in image
processing.
10. Arrays can be used in speech processing, where every speech
signal is an array.
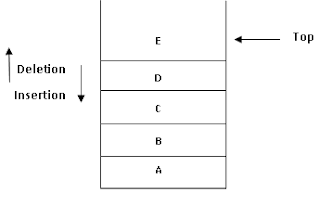
Stack:
It is defined as a list in which all the insertions and deletions operations are performed at one end called the TOP of stack.
Stack is an ordered collection of items in which insertion or deletion of items could be done, at one end, that is, at the top.
Fig: Representation of a Stack
For example, stack of dishes, stack of folded towels, Pile of books. Stack is a container, which follows LIFO principle.
- The insertion operation is known as PUSH.
- The deletion operation is known as POP.
Application of Stacks:
1. Stacks can be used for Evaluation
of Arithmetic Expressions.
2. Stacks can be used for Processing Function (Subprogram) Calls
3. Stacks can be used to check parenthesis matching in an
expression.
4. Stacks can be used for Evaluation
of postfix Expressions.
5. It can also be used to convert one form of expression to another
form. For example, converting Infix to Postfix or Infix to Prefix.
6. Recursion is one of the important applications of stack.
7. Stacks can be used for systematic
Memory Management.
8. String
reversal is also
another application of stack. We
push the characters of string one by one into stack and then pop character from
stack.
9. Stack is also heavily used for Syntax Parsing by most of the Compilers.
10. Stack data structures are used in backtracking problems. In Backtracking, while finding the every possible solution of
a problem, we store the solution of a previously calculated problem in Stack
and use that solution to solve the upcoming problems.
Queue:
It is defined as a list in which all the insertions (addition) and deletions operations are performed at REAR and FRONT respectively.
A queue is an ordered collection of items in which all insertions take place at one end, the Rear, where as all deletion takes place at other end, the Front.
Fig:
Representation of a Queue
In queue, the information is processed in FIFO (First In First Out) or FSFS (First Come First Served) way. For example, line of people waiting to purchase tickets.
The process of inserting items in
queue is called enqueueing and removing items
from a queue is called dequeueing.
There are three types of queues:
(i) Circular queue
(ii) Dequeue (Double Ended Queue)
(iii) Priority Queue.
Circular Queue:
Circular
Queue is also a linear data structure, which follows the
principle of FIFO(First In First Out), but instead of ending the
queue at the last position, it again starts from the first position after the
last, hence making the queue behave like a circular data structure.
Dequeue:
A Dequeue is a linear list in which the elements can be added or removed
at either end but not in middle.
Priority Queue:
A priority queue is a collection of elements such that each element has been assigned a priority and based on the order in which elements are inserted or deleted an processed.
Application of Queue:
1. Queue data structure is used in printers to maintain the order of pages while printing.
2. Queue is used for managing requests on a single shared resource such as CPU scheduling and disk scheduling
3. Queue is used in operating systems for handling interrupts. The interrupts are operated in the same order as they arrive, i.e., interrupt which comes first, will be dealt with first.
4. Queue is used in Process scheduling in Operating systems. Queues are used to implement round-robin scheduling algorithms in computer systems.
5. All types of customer service (like railway reservation) centers are designed using the concept of queues. Call center phone systems use Queues to hold people calling them in order until a service representative is free.
6. Queues are used in asynchronous transfer of data. When data is transferred asynchronously between two processes, queue is used for synchronization. For example: IO Buffers, pipes, file IO, etc
7. Nowadays computer handles multiuser, multiprogramming environment and time-sharing environment. In this environment a system (computer) handles several jobs at a time, to handle these jobs the concept of a queue is used.
8. Queues are used for Operation on Data Structure. Certain operations like ‘tree traversal’ and ‘Breadth first search uses queue for graph traversal’ involve the use of queues.
9. Queues are used as a Buffer Space in network, during transmission of data from source machine to destination.
10. Queues are used as buffers in most of the applications like MP3 media player, CD player, etc.
Linked List: It is defined as a linear collection of data elements called nodes, where each node consists of two parts i.e., information and pointer to next node. A list pointer variable FIRST or START contains the address of the first node in the list. The last node contains NULL pointer.
Fig: Representation of a Linked List
Types of Linked List:
There are different types of linked list . These are given below:(i) Singly Linked List
(ii) Doubly or two-way Linked List
(iii) Circular Linked List
(iv) Circular Doubly Linked List
Application of Linked List:
1. We can implement data structures like stacks and queues with the help of a linked list.
2. It is used in the implementation of graphs. Linked List helps in storing the adjacent vertices of a graph in adjacency list representation.
3. Linked list is used for DMA (Dynamic Memory Allocation).
4. Linked List is used to implement hash tables.
5. We can use linked lists for performing arithmetic operations on long int.
6. We can do polynomials manipulation with the help of a linked list by storing the constants in the nodes of the linked list.
7. Representation of a sparse tree matrix also requires a linked list.
8. Symbol table management in compiler design uses a linked list.
9. It is used to prevent collision in hashing.
10. In the browser when we want to use the back or next function to change the tab, it used the concept of a doubly-linked list.
11. Linked list is used in memory management. We can use a linked list to keep track of portions of memory available for allocation.
Non-Linear Data Structures:
Elements of non-linear data structures are stores and accessed
in non-linear order. These are multilevel data structures.
Examples of non-linear data structure are: Tree and Graph
Tree: A tree is a nonlinear hierarchical data structure that consists of nodes connected by edges.
A tree has the following properties:
1. The tree has one node called root. The tree originates from this, and hence it does not have any parent.
2. Each node has one parent only but can have multiple children.
3. Each node is connected to its children via edges.
Representation of Tree:
Fig: A
general tree
Here
the root of
the tree is A.
There are three subtrees of the root A, with roots B,D and G. The root B has one subtree. The root C has
empty subtree. The root D and G have two and three subtrees respectively. The
nodes (except root) having no subtrees are called leaf nodes or
terminal nodes. In the above tree, C,E,F,H,I,J are the leaf
nodes or terminal nodes. Any node (except the root and leaf nodes) is called non-terminal node. Here, B,D and G are the non-terminal nodes.
The node having at least a child node is called an internal node. G is an internal node.
Level of a Node: The level of a node is equal to the length of
the path from the root to the node. The root of
the tree has level=0.
For
example, in above tree the levels are:
Level
of A=0
Level of
B,D,G=1
Level
of C,E,F,H,I,J=2
Degree of a node: The degree of a node is the number of
children it has. The degree of a leaf is 0. For example in above tree the
degree of node D is 2.
Degree of a tree: The degree of a tree is the maximum of its
node degrees. The degree of tree in above figure is 3.
Height/Depth of a tree: If level of the root is denoted by 0, then
Height/Depth
of tree =1+ maximum levels of all nodes in the tree
The
height/depth of tree given in above figure is 3.
Parent and child relationship: In above tree, the node A is parent of B, D and G.
B, D
and G are called children of A.
The children nodes of a given parent node are called siblings or brothers.
Ancestor of a Node: Any predecessor nodes on the path of the root to that
node are called Ancestors of that node. For example, in the above tree A
and D are the ancestor of E.
Descendant: Any successor node
on the path from the leaf node to that node. B,C are the descendants of
the node A.
More Tree Terminology:
- The depth of a node is the number of edges from the root to the node.
- The height of a node is the number of edges from the node to the deepest leaf.
- The height of a tree is a height of the root.
- A full binary tree.is a binary tree in which each node has exactly zero or two children.
- A complete binary tree is a binary tree, which is completely filled, with the possible exception of the bottom level, which is filled from left to right.
Advantages of Trees:
Trees are so useful and frequently used, because they have some very serious advantages:
- Trees reflect structural relationships in the data
- Trees are used to represent hierarchies
- Trees provide an efficient insertion and searching
- Trees are very flexible data, allowing to move subtrees around with minimum effort
Binary Tree:
A binary tree is a hierarchal data structure in which each node has at most two children. The Binary tree means that the node can have maximum two children. Here, binary name itself suggests that 'two'; therefore, each node can have either 0, 1 or 2 children.
A binary tree is
simply a tree in which each node can have at most two children. A binary tree is made of nodes, where each node
contains a "left" reference, a "right" reference, and a
data element. The topmost node in the tree is called the root.
A
tree is called a binary tree if it has a finite set of nodes that is either
empty or consists of a root and two disjoint subsets, each of which itself is a
binary tree. The two subsets are called the left subtree and the right
subtree of the original tree.
Binary
trees are different from general trees. A binary tree has left and right
subtrees, whereas, in general trees there is no left or right subtree.
Fig: Binary Tree
The above tree is a
binary tree because each node contains the at most two children. Here, A is the
root of the tree and it has two subtrees. The left subtree has
root B and it also has two subtrees are D and E. The right subtree has root C and it has one
subtree F. Subtrees D,E and F has no subtrees.
Properties of Binary Tree:
1. The drawing of every
binary tree with n elements, n>0, has exactly n-1 edges.
2. A binary tree of height h,
h>=0, has at least h and at most 2h -1 elements in it.
3. A binary tree can have a
maximum of 2l nodes at level l if the level of the root is zero.
4. The height of a binary
tree that contains n, n>=0, elements is at most n, at least log2(n+1)
5. In a binary tree with n
nodes, minimum possible height or minimum number of levels are log2(n+1).
If we consider that the height of leaf node is considered as 0, then the
formula will be log2(n+1)-1.
6. A binary tree with ‘L’
leaves has at least log2(L+1) number of levels.
7. If a binary tree has 0 or 2 children, then
number of leaf nodes are always one more than nodes with two children.
Types of Binary Tree:
There are various types of binary trees, and each of these binary tree types has unique characteristics.
Full Binary Tree: The full binary tree is also known as a strict binary tree. A binary tree is said to be a full binary tree when each node has zero or two children. We can say it is a binary tree in which all nodes except leaf nodes have two children.
Complete Binary Tree: A binary tree is referred to as a complete binary tree when all of its levels are completely filled except the lowest level of the tree. Also, in the last or the lowest level of this binary tree, every nodes should possibly reside on the left side.
Perfect Binary Tree: A perfect binary tree is a special type of binary tree in which all the internal nodes have two children and every external or leaf node is at the same level.
Balanced Binary Tree: A balanced binary tree also referred to as a height-balanced binary tree is also a special type of binary tree in which the difference of height between the left and the right subtrees for each node is at most one.
The above tree is a balanced binary tree because the difference between the left subtree and right subtree is not greater than 1.
Skewed Binary Tree: A binary tree is said to be a skewed binary tree if all of its internal nodes have exactly one child, and either left children or right children dominate the tree. There exist two types of skewed binary trees: left-skewed binary tree and the right-skewed binary tree.
Binary Search Tree:
A special kind of binary tree is called a binary search tree. In binary search tree, the data value stored in any node is greater than the data value stored in its left child and less than the data value stored in its right child node, assuming that there are no duplicate values.
The formal definition of a binary search tree is given below:
A binary search tree is a binary tree that may be empty. A non-empty binary search tree satisfies the following properties:
1. Every element has a key (or value) and no two elements have the same key; therefore all keys are distinct.
2. The keys (if any) in the left subtree of the root are smaller than the key in the root.
3. The keys (if any) in the right subtree of the root are larger than the key in the root.
4. The left and right subtrees of the root are also binary search trees.
Fig: A binary search tree
Tree Traversal Methods:
A traversal is a process that visits all the nodes in the tree. The term 'tree traversal' means traversing or visiting each node in the tree exactly once and performing some operations on it. There are three ways which we use to traverse a tree:
- Pre-order Traversal
- In-order Traversal
- Post-order Traversal
Pre-order Traversal: In this traversal method, the root node is visited first, then the left subtree and finally the right subtree. As the root node is traversed before (or pre) the left and right subtree, it is called preorder traversal.
In-order Traversal: In this traversal method, the left subtree is visited first, then the root and later the right sub-tree. As the root node is traversed between the left and right subtree, it is named inorder traversal.
If a binary tree is traversed in-order, the output will produce sorted key values in an ascending order.
Post-order Traversal: In this traversal method the left subtree is visited first, then the right subtree and finally the root node. As the root node is traversed after (or post) the left and right subtree, it is called postorder traversal.
As an example consider the following tree and
its three traversals:
Pre-order: 8, 5, 9, 7, 1, 12, 2, 4, 11, 3
In-order: 9, 5, 1,
7, 2, 12, 8, 4, 3, 11
Post-order: 9, 1,
2, 12, 7, 5, 3, 11, 4, 8
Graph: Graph is a non-linear data structure. It is defined as a set of nodes (or vertices) and a set of arcs (or edges) where each arc in it is specified by a pair of nodes.
A graph G consists of two things:
(i) A set V of elements called nodes ( or vertices)
(ii) A set E of edges (or arcs) such that each edge e in E is identified with a unique (unordered) pair [u,v] of nodes in V, denoted by e=[u,v].
Fig. Graph representation
In case the arcs are ordered
pairs, the graph is said to be a directed graph. A directed graph is
also called diagraph.
Weighted Graph: A graph is said to be weighted graph if every edge in the graph is assigned some data.
(i) Breadth-First
Search (BFS)
(ii) Depth
First Search (DFS)
There are three ways to represent a graph in memory of a computer:
(i) Adjacency
Matrix Representation
(ii) Adjacency
List Representation
(iii) Multi
List Representation
Tree vs Graph Data Structure:
|
Tree |
Graph |
|
It is a non-linear data structure. |
It is also a non-linear data structure. |
|
It is a collection of nodes and edges |
It is a collection of vertices/nodes
and edges. |
| There is a unique node called root in trees. |
There is no unique node called root in
graph. |
|
Usually, a tree can have several child nodes, and in the
case of binary trees, every node can
have at the most two child nodes. |
Each node can have several edges. |
|
It does not create any loop or cycle. |
In graph, loop or cycle can be formed. |
|
It is a network model. |
It is a hierarchical model because nodes are arranged in
multiple level, and that creates a hierarchy. |
|
Trees have simple structures |
Graphs can have more complicated structures since they can
have loops. |
|
We can traverse a tree using in-order, pre-order, or
post-order traversal methods. |
For graph traversal, we use Breadth-First Search (BFS), and
Depth-First Search (DFS). |
Difference between Linear and Non-linear Data Structures:
|
Linear Data
Structure |
Non-Linear
Data Structure |
|
In linear data structure, the elements are arranged in
linear order, one after
the other |
In non-linear data structure, the data elements are
arranged in non-linear order. |
|
It is single level data structure |
It is multi-level data structure |
|
Linear data structures are easy to implement. |
Non-linear data structures are difficult to implement as
compared to the linear data structures. |
|
In linear data structure, data elements
can be traversed in a single run only. |
In non-linear data structure, data
elements can’t be traversed in a single run. It requires multiple runs. |
|
In a linear data structure, memory is
not utilized in an efficient way. |
In a non-linear data structure, memory
is utilized in an efficient way. |
|
Linear data structures work well mainly in the development
of application software. |
Non-linear data structures work mainly well in image
processing and Artificial Intelligence. |
|
Linear data structures are useful for
simple data storage and manipulation. |
Non-linear data structures are useful
for representing complex relationships and data hierarchies, such as in
social networks, file systems, or computer networks. |
|
Example: array, stack, queue, linked
list. |
Example: trees, graphs. |
Operations on Data Structure:
Every data structure contains the set of data elements. Traversing the data structure means visiting each element of the data structure in order to perform some specific operation like searching or sorting.
Searching: Search is an activity in which a particular record or item is to be found. The process of finding the location of an element within the data structure is called Searching.
Data stored in an organized manner requires to be accessed for processing. Locating a particular data item in the memory involves searching the data item. Searching is a technique where the memory is scanned for the required data.
Insertion: Insertion can be defined as the process of adding the elements to the data structure at any location. Insertion is a process in which a new element is added into the structure.
Deletion: The process of removing an element from the data structure is called deletion. We can delete an element from the data structure at any random location.
Sorting: Sorting is a process in which all elements are arranged in a specific order so that each item can be retrieved easily. Sorting means arranging the elements in some specific order, i.e., either ascending or descending order.
The term sorting refers to the operation of arranging data in some given order, such as increasing or decreasing with numerical data or alphabetically, with character data.
Merging: Merging is a process in which two structures are combined into a single




























0 Comments
if you have any doubts plz let me know...